Функция вида  , где
, где  называется квадратичной функцией.
называется квадратичной функцией.
Графиком квадратичной функции является парабола.

1 уровень
1. На разных чертежах изобразите графики функций:
 , где
, где  называется квадратичной функцией.
называется квадратичной функцией.Графиком квадратичной функции является парабола.
Вершиной параболы называется точка

Если коэффициент а>0, то ветви параболы направлены вверх, если a<0, то ветви параболы направлены вниз.
Квадратичную функцию  всегда можно привести у виду y=a(x-s)2+t
всегда можно привести у виду y=a(x-s)2+t

Для построения параболы необходимо:
1) Найти координаты вершины
2) Построить ось симметрии, проанализировать куда направлены ветви параболы
3) Найти точки пересечения параболы с осью Ox (нули), если они есть, решив уравнение  4) Найти точку пересечения с осью Оу, решив уравнение
4) Найти точку пересечения с осью Оу, решив уравнение 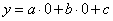
 всегда можно привести у виду y=a(x-s)2+t
всегда можно привести у виду y=a(x-s)2+t
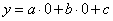
D>0
|  |  |
D=0
|  |  |
D<0
|  |  |
Домашнее задание
1 уровень
1. На разных чертежах изобразите графики функций:
y=3x2+8х-3; y=x2-х+3.
2. Укажите координаты точек пересечения графика функции с осями ОХ и ОУ:
2. Укажите координаты точек пересечения графика функции с осями ОХ и ОУ:
а) y=2x2-5х-3; б) y=-3x2+х+70.
2 уровень
2 уровень
1. На разных чертежах изобразите графики функций:
y=-0,5x2-х-0,5; y=x2-2х+3.
2. Для каждой параболы найдите координаты ее вершины:
а) y=2x2-5х-3; б) y=-3x2+х+70.
3 уровень
2. Для каждой параболы найдите координаты ее вершины:
а) y=2x2-5х-3; б) y=-3x2+х+70.
3 уровень
1. На разных чертежах изобразите графики функций:
y=2x2-3х-2; y=-0,5x2+2х-3; y=-3x2+8х+3.
2. Найдите координаты вершины параболы и укажите точки пересечения графика функции с осями ОХ и ОУ:
а) y=-0,5x2-х-0,5; б) y=x2-2х+3; в) y=x2-4х+4.
3.При каких значениях р вершина параболы
y=9x2+6х-р располагается:
а) ниже оси ОХ; б) выше оси ОХ; в) на оси ОХ?
4 уровень
2. Найдите координаты вершины параболы и укажите точки пересечения графика функции с осями ОХ и ОУ:
а) y=-0,5x2-х-0,5; б) y=x2-2х+3; в) y=x2-4х+4.
4 уровень
1. На разных чертежах изобразите графики функций:
y=x2-4х+4; y=1/3x2-2х+4; y=-x2-6х-9.
2. Найдите координаты вершины параболы и укажите точки пересечения графика функции с осями ОХ и ОУ:
а) y=-3x2+х+70; б) y=2x2+8-8х; в) y=8x2-3х+28.
3.При каких значениях р вершина параболы
1) y=7x2-5х+4р; 2) y=4x2+рх+25 располагается:
2. Найдите координаты вершины параболы и укажите точки пересечения графика функции с осями ОХ и ОУ:
а) y=-3x2+х+70; б) y=2x2+8-8х; в) y=8x2-3х+28.