32. Функция аx^2+c

График функции y = ax² + с.

Графиком функции y = ax² + с является парабола, которую можно получить из графика функции y = ax²   с помощью параллельного переноса вдоль оси y на с единиц вверх, если   с > 0, или на –с единиц вниз, если с < 0.

Пример: построить график функции y = 2x² + 4.
Это значит, что парабола, которая является графиком функции y = 2x² , перемещается на четыре единицы вверх по оси y. Разумеется, при этом все значения y закономерно увеличиваются на 4.

Вот таблица значений функции y = 2x²:

x	-4	-3	-2	-1	0	1	2	3	4
y	32	18	8	2	0	2	8	18	32

А вот таблица значений y = 2x² + 4:

x	-4	-3	-2	-1	0	1	2	3	4
y	36	22	12	6	4	6	12	22	36

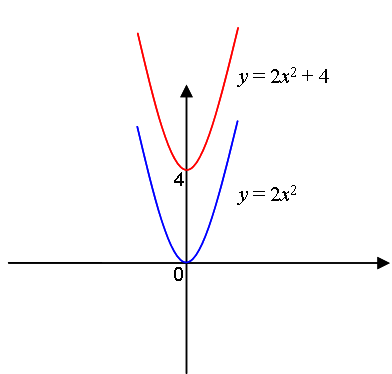
Мы видим по таблице, что вершина параболы второй функции на 4 единицы выше вершины параболы первой (ее координаты 0;4). А значения y второй функции на 4 больше значений y первой функции.

Домашнее задание

1 уровень
1. На одном чертеже изобразите графики функций y=2x²;  y=2x²-1;  y=2x²+2.

Укажите:
а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ.

2. Задайте формулой функцию, график которой получается с помощью сдвига параболы y=25x² вдоль оси ОУ на:
а) 9 единиц вниз; б)  8 единиц вверх.

2 уровень
1. На одном чертеже изобразите графики функций y=-2x²;  y=-2x²+4;  y=-2x²-3.

Укажите:
а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ.

2. Задайте формулой функцию, график которой получается с помощью сдвига параболы y=100x² вдоль оси ОУ на:
а) 99 единиц вниз; б)  24 единицы вверх.

3 уровень
1. Как из графика функции y=0,25x² можно получить график функции:
а)  y=0,25x²-3;   б) y=0,25x²+2;   в) y=-0,25x²+1;  г)  y=-5-0,25x²

2. Используя изображение параболы, напишите уравнение и укажите для функции ее свойства: а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ;
д) значения х, при которых y<0;
е) значения х, при которых y>0;
ж) значения х, при которых y=0.

3. При каких значениях постоянной р график функции y=-6x²+р проходит через точку:
а) А(0; 1);   б) В(-2; 48);   в) С(1/3; -12)?


4 уровень
1. Как из графика функции y=0,75x² можно получить график функции:
а)  y=-0,75x²+3;   б) y=0,75x²-5;   в) y=0,75x²+4;  г)  y=-3-0,75x²

2. Используя изображение параболы, напишите уравнение и укажите для функции ее свойства: а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ;
д) значения х, при которых y<0;
е) значения х, при которых y>0;
ж) значения х, при которых y=0.

3. При каких значениях а график функции y=аx²-4 проходит через точку:
а) А(1; 0);   б) В(-2; -20);   в) С(1/5; 11)?