График функции y = a(x – s)2.
Вершина параболы - (s; 0).
Ось симметрии: x= s.
1 уровень
1. На одном чертеже изобразите графики функций
а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ.
2. Задайте формулой функцию, график которой получается с помощью сдвига параболы y=3,5x2 :
а) вдоль оси ОХ на 5 единиц влево; б) вдоль оси ОХ на 7 единиц вправо.
3 уровень
1. Как из графика функции y=16,8x2 можно получить график функции:
а) y=16,8(x-12,9)2; б) y=16,8(x+4,5)2; в) y=4,2(2x-8)2
2. Используя изображение параболы, напишите уравнение и укажите для функции ее свойства: а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ;
д) значения х, при которых y<0;
е) значения х, при которых y>0;
ж) значения х, при которых y=0.
3. Укажите координаты вершины параболы и запишите уравнение оси симметрии параболы:
а) y=-16(x-2)2; б) y=25(x+24)2; в) y=9x2+1,8
Графиком
функции y = a(x – s)2 является парабола, которую можно получить из графика
функции y = ax2 с помощью параллельного переноса вдоль оси x на s единиц вправо, если s>0, или на s единиц влево, если s<0.
Вершина параболы - (s; 0).
Ось симметрии: x= s.
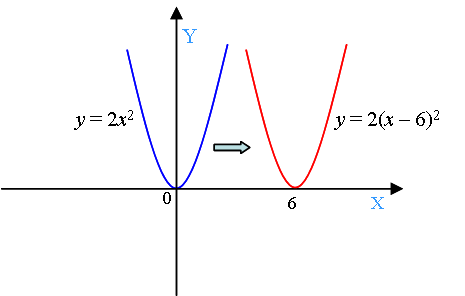
Пример: построить
график функции y = 2(x – 6)2.
Это значит,
что парабола, которая является графиком функции y = 2x2,
перемещается на шесть единиц вправо вдоль оси x (на графике – красная
парабола).

Домашнее задание
1 уровень
1. На одном чертеже изобразите графики функций
y=2x2; y=2x2+1; y=2(х+1)2; y=2(х-4)2;.
а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ.
2. Задайте формулой функцию, график которой получается с помощью сдвига параболы y=-6,4x2 :
а) вдоль оси ОХ на 6 единиц влево; б) вдоль оси ОХ на 4 единицы вправо.
2 уровень
1. На одном чертеже изобразите графики функций
а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ.
2. Задайте формулой функцию, график которой получается с помощью сдвига параболы y=-6,4x2 :
а) вдоль оси ОХ на 6 единиц влево; б) вдоль оси ОХ на 4 единицы вправо.
2 уровень
1. На одном чертеже изобразите графики функций
y=-3x2; y=-3x2+2; y=-3(x+2)2; y=-3(х-1)2;.
а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ.
2. Задайте формулой функцию, график которой получается с помощью сдвига параболы y=3,5x2 :
а) вдоль оси ОХ на 5 единиц влево; б) вдоль оси ОХ на 7 единиц вправо.
3 уровень
1. Как из графика функции y=16,8x2 можно получить график функции:
а) y=16,8(x-12,9)2; б) y=16,8(x+4,5)2; в) y=4,2(2x-8)2
2. Используя изображение параболы, напишите уравнение и укажите для функции ее свойства: а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ;
д) значения х, при которых y<0;
е) значения х, при которых y>0;
ж) значения х, при которых y=0.
а) y=-16(x-2)2; б) y=25(x+24)2; в) y=9x2+1,8
г) y=-6x2-3; д) y=-(x+2)2; е) y=(8-х)2
4 уровень
1. Пересекает ли график функции y=-6(x+1)2 прямую:
а) y=2; б) y=-2х-6?
2. Используя изображение параболы, напишите уравнение и укажите для функции ее свойства: а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ;
д) значения х, при которых y<0;
е) значения х, при которых y>0;
ж) значения х, при которых y=0.
3. При каких значениях р график функции y=р(x+1)2 проходит через точку:
а) А(-3; -8); б) В(4; 25); в) С(-34; 0)?
4 уровень
1. Пересекает ли график функции y=-6(x+1)2 прямую:
а) y=2; б) y=-2х-6?
2. Используя изображение параболы, напишите уравнение и укажите для функции ее свойства: а) координаты вершины параболы;
б) направление ветвей параболы;
в) координаты точек пересечения параболы с осью ОХ;
г) координаты точек пересечения параболы с осью ОУ;
д) значения х, при которых y<0;
е) значения х, при которых y>0;
ж) значения х, при которых y=0.
а) А(-3; -8); б) В(4; 25); в) С(-34; 0)?

