Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
1 уровень
Упражнение 41 стр. 102, упражнение 33 стр. 101
2 уровень
Упражнение 42 стр. 102, упражнение 34 стр. 101
3 уровень
Упражнения 31, 35 стр. 101
4 уровень
Упражнения 32, 36, 37 ( к № 37: медиана, проведенная из прямого угла прямоугольного треугольника равна половине гипотенузы) стр. 101.
Таблица значений синуса, косинуса, тангенса и котангенса для углов от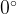 
до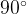 
.
Выучить!!! до .
Основное тригонометрическое тождество: sin2a+cos2a=1.
Теорема. При возрастании острого угла синус этого угла увеличивается, а косинус уменьшается.
Домашнее задание
глава 3, параграф 5
Задания находятся в книге В.В. Казакова "Наглядная геометрия. Опорные конспекты. Контрольные вопросы. Задачи на готовых чертежах. 8 класс"
Домашнее задание выполняется в рабочей тетради. Должен быть рисунок, записано "Дано", "Найти" или "Доказать", "Решение".
1 уровень
Упражнение 41 стр. 102, упражнение 33 стр. 101
2 уровень
Упражнение 42 стр. 102, упражнение 34 стр. 101
3 уровень
Упражнения 31, 35 стр. 101
4 уровень
Упражнения 32, 36, 37 ( к № 37: медиана, проведенная из прямого угла прямоугольного треугольника равна половине гипотенузы) стр. 101.
